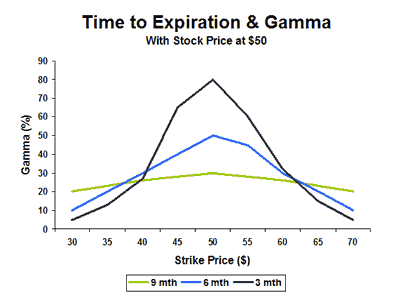
Vega is the greek that represents an option’s sensitivity to implied volatility.
More specifically, vega measures the change in an option’s price for every one percentage point change in implied volatility. So if an option’s vega is 0.10 and its implied volatility rises 1%, the option’s price will increase $0.10. On the other hand, if implied volatility falls 1%, the option’s price will decrease $0.10.
Vega is positive for both calls and puts, and is most sensitive when an option is at the money.
As a quick refresher, implied volatility (IV) is a forward-looking value that represents the market’s best guess on future price movement in an underlying asset.
While everything else that goes into an option’s price is known: interest rates, dividends, time to expiration, and stock price, implied volatility is unknown. However, you can solve for implied volatility using the current price of an option.
Unlike delta, which measures how an option’s price will change based on an actual price change in the underlying stock, vega estimates how much an option will gain or lose based on an increase or decrease in the option’s implied volatility.
When the market expects higher volatility from a stock — perhaps ahead of earnings, which can trigger big moves on the charts, an option’s IV, which is expressed as a percentage, will be higher. On the flip side, if the stock is expected to stagnate during the option’s lifetime, its IV will be lower.
The other things that factor into IV are the time until expiration and the stock’s price.
The more time an option has for the stock to make a big move, the higher that contract’s IV. Therefore, shorter-dated options are less susceptible to IV changes.
The prices of out-of-the-money and at-the-money options feel fluctuations in IV the hardest, because they’re made up of only extrinsic value. The price of in-the-money options don’t fluctuate as much with IV changes, as their premiums are largely made up of intrinsic value.
When a trader is long an option, they are said to be long vega, and will therefore benefit from an uptick in volatility. And when a trader is short an option, they are said to be short vega, and will therefore benefit from a decrease in volatility.
It’s important to not confuse implied volatility with historical volatility, which measures how much the asset has actually moved in the past. However, implied volatility is often compared to a stock’s historical volatility to determine if an option’s price is expensive or cheap, relatively speaking.
Additional points to keep in mind with regard to vega:
- Vega can increase or decrease without the price of the underlying asset changing, due to changes in implied volatility.
- Vega can increase in reaction to quick moves in the underlying asset.
- Vega falls as the option gets closer to expiration.
Wrapping Up
Implied volatility is a major factor determining an option’s price. When you buy an option, you want implied volatility to increase, so you can sell the option at a higher price than you initially paid.
On the flip side, when you sell options, you want implied volatility to decrease, so that you can buy the option back at a lower cost.
These changes in implied volatility — and how it impacts an option’s price — are measured by “vega,” which is just one of the “Greeks” options traders should understand before pulling the trigger on a trade.