Gamma

Gamma is a second derivative of an option’s price that measures the rate of change in delta over time.

Since delta values shift with the underlying asset’s price, gamma is applied and used to measure the rate of change in delta based on a $1 move in the underlying security. It’s a gauge of the velocity of potential change in delta. The larger the gamma, the faster the option’s delta is going to move.

Similar to delta, gamma is constantly changing with the underlying stock’s movements. The values of gamma are generally highest for at-the-money and soon-to-expire options, and they are lowest for out-of-the-money options. The exception is options that are deep in the money or out of the money, which have gamma values closer to 0.

Additionally, it’s important to remember that all long options have a positive gamma, while all short options have a negative gamma to account for direction easily.

Still mixed up?

Think of these metrics in a way that is related to physics acting on a car. The car is traveling at a speed of 50 miles per hour (delta), and requires accelerating by 10 miles per hour (gamma) to reach the new speed it is needed to be traveling at.

In other words, the speed the car is currently traveling is also known as delta, and the acceleration or deceleration it will experience to change the speed is known as gamma.

Another way to think of gamma is by a measure of the stability of an option’s probability. If delta represents the probability of being in the money at expiration, gamma represents the stability of that probability over time.

Example of Gamma
Suppose Apple (AAPL) is the car in the above example, and is currently trading at $100. Meanwhile, the 105-strike call option is priced at $5. Now, let’s assume it has a delta of 0.50 (the speed of the car) and a gamma of 0.10 (the acceleration of the car).

If the stock price moves up by $1 to $101, then the new option price is $5.50, based on its delta of 0.50. At this point, the new delta would increase by 0.10 to 0.60, based on the value of gamma.

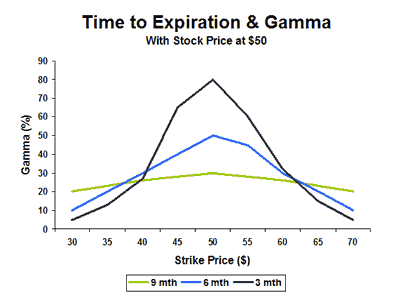
How Time Impacts Gamma
As expiration nears, the gamma of at-the-money options will rise in value, while the gamma of in-the-money and out-of-the-money options will fall.

Wrapping Up
Gamma is an important metric because it corrects for convexity issues of delta based on the move in the underlying equity, and lets you know how much an option’s delta should change as the stock price changes.

Remember:

1. Gamma is smallest for deep out-of-the-money and deep-in-the-money options.
2. Gamma is highest when the option gets near the money.
3. Gamma is positive for long options and negative for short options.